Huddersfield Town lock horns with Premier League opposition this weekend when they travel to Burnley in the FA Cup.
Carlos Corberan's side are unbeaten in six Championship fixtures heading into the tie and will be full of confidence that they can claim a Premier League scalp at this early stage of the competition.
Given Huddersfield's strong position in the league table, there's no need for Corberan to overhaul his squad. Instead, it makes sense to see a mix of fringe players with a couple of first-teamers to match.
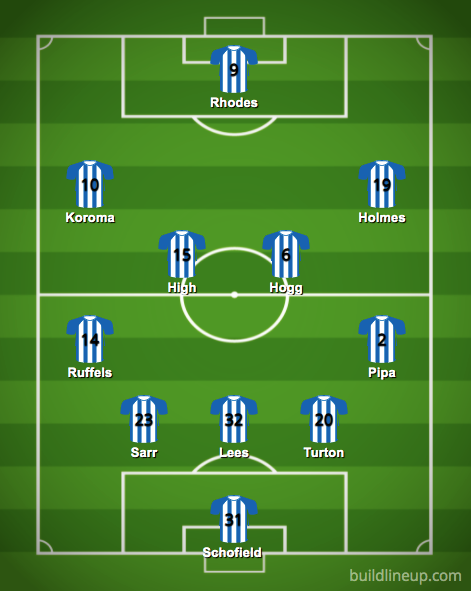
As our graphic above shows, Lee Nicholls might earn himself a rest at Turf Moor, with Ryan Schofield potentially coming into the side in goal.
It should be a back-three once more, with Naby Sarr, Tom Lees and Ollie Turton lining up from left-to-right, whilst Levi Colwill and Matty Pearson take a welcome break.
The FA Cup feels like an opportunity for Josh Ruffels to get a chance ahead of Harry Toffolo, whilst it's certainly the right time for Pipa to make his first start of the season.
Jonathan Hogg will play some minutes and, therefore, could start alongside Scott High in a dynamic midfield duo.
In terms of the attacking set-up, Jordan Rhodes could well be the focal point, with Josh Koroma and Duane Holmes selected to buzz around him and provide some width.